Индивидуальная работа учителя математики

Автор: Бондарева Татьяна Устиновна, учитель математики МБОУ «СОШ № 8»

Основным выражением индивидуальности взрослого человека являются его дарования и способности, творческое мышления, жизненная позиция, опыт деятельности и отношений; важнейшее проявление индивидуальности ребенка — восприимчивость к обучению и воспитанию. Педагоги часто замечают, что одинаковые воспитательные меры на одних учащихся оказывают благородное влияние, на других действуют слабо, а иногда даже и отрицательно. Это зависит не только от педагога, но и от активности самого ребенка, его заинтересованности в результатах обучения и воспитания, от уровня его общего развития и воспитанности, психического состояния в данный момент.

Стимулирование волевых усилий, направленных на достижение качественных показателей в учении, начинается с индивидуальных консультаций и применения следующих приемов работы.

Мобилизация внутренних сил на выполнение задания. Перед учеником раскрываются его возможности, умения, необходимость предстоящей работы лично для него, перспективы его усилий.

Активизация целевой установки. Поставленную учеником цель следует глубже мотивировать, а затем разработать с ним правила повседневного эффективного труда (начатое дело доводить до конца, не браться за несколько дел сразу, прилежно выполнять любую работу, анализировать ошибки, переделывать неудачно выполненную работу).

Одобрение первых успехов. Учитель несколько завышает оценку положительных результатов деятельности ученика с тем, чтобы у него возникло желание совершенствовать выработанные навыки учения и труда.

Учет самолюбия. Ученики с проявлениями лености очень болезненно реагируют на обнаружение их недостатка перед другими. Они отнюдь не равнодушны к своим неудачам, как это принято считать, напротив, они осознают и очень тяжело переживают то, что из-за недостатка воли не могут добиться успеха на в одной области. Они остро нуждаются в повседневной помощи взрослых, но если вместо нее выслушивают упреки и наставления, то постепенно озлобляются, отказываются делать то, что не получается. Целесообразно поэтому давать таким ученикам специальные задания, опрашивать их отдельно, сообщая классу только положительные результаты до тех пор, пока ученик не почувствует уверенности в своих силах.

Предупреждение ошибок путем стимулирования самоконтроля. Используя этот прием, учитель стремится помочь ребенку разобраться в его ошибках, предупредить их: «Подумай, прочитай вот это правило. Ошибка здесь. Постарайся ее не повторять в следующий раз».

На каждом этапе урока большое значение я придаю организации самостоятельной работы учащихся, учитывая, что главная задача — научить их на основе усвоения определенных фактов их разделов программы по математике добывать новые знания и закреплять старые.

Планируя самостоятельную работу, я намечаю задания для учащихся в соответствии с их уровнем знаний, умений и навыков, определяю меру руководства индивидуальной работой учащихся. В планах намечаю перспективу работы как с отдельными учащимися, так и с группами, определяю цель работы, ее содержание и методику.

Овладение приемами самостоятельной работы у учащихся происходит успешнее, если необходимую помощь от учителя они получают в письменном виде.

Виды инструктажа:

1. Указание плана работы (приемы, последовательность, основные этапы).
2. Сообщения, указания к решению, образцы способа решения.
3. Показ схем, приводящих к правильному выводу:
   а) вспомогательные вопросы,
   б) алгоритм решения.

4. Подача подтверждающей информации:
а) ответы,
б) образцы решения.

При сообщении домашних заданий слабо успевающим учащимся предлагаю найти параграф учебника, ознакомиться с текстом задачи, задать вопросы; обращаю их внимание на важные и трудные моменты, рекомендую последовательность выполнения домашнего задания.

Общеизвестно, что одной из самых больших трудностей при изучении математики является то, что каждая новая тема опирается на обширный ранее изученный материал и незнание некоторых вопросов, даже весьма частных, влечет за собой непонимание нового материала. поэтому перед изучением темы важно проанализировать, что должны знать и уметь учащиеся. Полезно дать каждому задание на повторение материала, причем задание должно содержать не только теоретический материал, но и задачи.

Виды дифференцированных заданий по математике

1) Задания с алгоритмическими предписаниями

«Под алгоритмом обычно понимают точное общепринятое предписание о выполнении в определенной (в каждом конкретном случае) последовательности элементарных операций (из некоторой системы таких операций) для решения любой из задач, принадлежащих некоторому классу (или типу)».

Основные черты, характеризующие алгоритм:

• указания, входящие в предписание, однозначно определяют характер и условия каждого действия;
• посредством алгоритма может быть выполнено не одно задание (решен пример), а целый класс подобных заданий;
• с помощью алгоритма всегда можно прийти к правильному результату.

Пример задания: Решить уравнение:

х³ + 3х (х — 8) = 2х (3 — х + 0,5ײ) + 1

1. Привести уравнение к стандартному виду.
2. Найти дискриминант уравнения.
3. По формуле корней квадратного уравнения вычислить его корни.

2) Задания с сопутствующими указаниями, инструкциями

В этих заданиях даются указания и советы частичного характера, определяющие выбор способа действия, активизирующие внимание на центральном звене задания.

Задание. Найти производную сложной функции:

у = (2х — 1)³

Решение:

1. Обозначить 2х — 1 = и, тогда у = и³.
2. Найти производную f’(u) = (u³)’.
3. Найти производную φ’(х) = (2х — 1)’.
4. Производная сложной функции равна у = f’(u)^.φ’(х).

3) Задания с выбором ответа

Это такие задания, в которых предлагается пример или задача и варианты ответов. Учащийся выбирает тот ответ, который, по его мнению, соответствует данному заданию.

Задание. Координаты точки пересечения графика функции y= (x³+5x-6)/(x-3) с осью ординат равны:

1. (1; 0)
2. (0; 1)
3. (0; 2)
4. (2; 0).

4) Задания с применением классификации

К данному виду можно отнести задания, в которых учащемуся нужно по ряду признаков отнести пример или задачу к определенному классу.

Задание. Выписать уравнения, решаемые способом приведения к общему основанию, и решить их:

2^5х = 4^2х+1

3^х+2 + 3^х+1 + 3^х = 39

3^2х — 10 ^. 3^х + 9 = 0

2^3х — 0,5 = 0

13^х = 1

5^3х = 25^х+0,5

8^х = 4^х-1

4^х — 5 ^. 2^х — 24 = 0

5) Задания с выполнением некоторой их части

Учащимся предлагается задание (содержит готовое решение некоторых действий), решение которого нужно закончить. В готовом виде даются те части решения, которые представляют на определенной ступени трудность для учащихся.

Задание. Отрезок MN, равный 12см, расположен вне плоскости . Концы отрезка отстоят от плоскости на расстоянии MM₁ = 14 см, NN₁ = 20 см. Найти угол между MN и плоскостью.

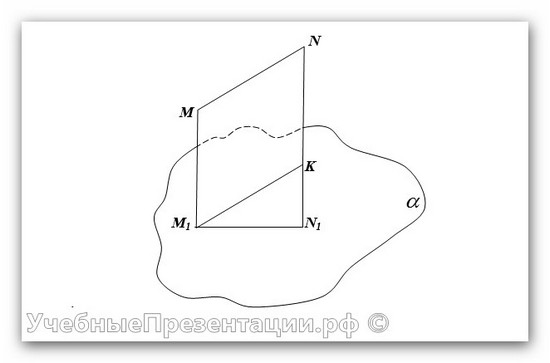
Решение.

Проведем M₁K ‌‌‌‌|| MN.

угол KM₁ N₁ — искомый.

6) Задания с образцом выполнения

Для усвоения приема решения показательных уравнений сведением их к квадратным могут быть предложены задания с развернутым образцом решения.

Задание. Решить уравнение 4^х + 3 ^. 2^х — 4 = 0.

Образец решения уравнения 2 ^. 2^х + 4^х = 80.

1. 4^х = 2^2х
2. 2 ^. 2^х + 2^2х = 80
3. 2^х = у; 2^2х = у²
4. 2у + у² = 80
5. 2^х = у₁2^х = −10 нет решений, т.к. 2^х > 0
6. 2^х = у₂2^х = 8 2^х = 2³ х = 3

Ответ: х = 3.

7) Задания с вспомогательными вопросами

Дидактическая цель применения вопросов в заданиях состоит в том, чтобы помочь учащемуся воспроизвести знания, необходимые для нахождения способа решения данного задания или побудить внимание учащегося мыслить в нужном направлении.

Задание. Доказать признак параллельности прямой и плоскости.

Вопросы к доказательству:

1. Какую плоскость надо построить? Сколько таких плоскостей можно провести? Почему?
2. Каково взаимное положение данной и построенной плоскостей?
3. Каким методом доказывается теорема?
4. Как будет расположена прямая по отношению к линии пересечения плоскостей? Что отсюда следует?
5. Какое противоречие с условием получено?
6. Сделать вывод.